设实数m.n.x.y满足m2+n2=a.x2+y2=b.其中a.b为正的常数.则mx+ny的最大值是( )A．$\frac{a+b}{2}$B．$\sqrt{a•b}$C．$\frac{2ab}{a+b}$D．$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

20．设实数m、n、x、y满足m²+n²=a，x²+y²=b，其中a、b为正的常数，则mx+ny的最大值是（　　）

A．

$\frac{a+b}{2}$

B．

$\sqrt{a•b}$

C．

$\frac{2ab}{a+b}$

D．

$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$

分析可利用三角换元求解．令m=$\sqrt{a}$cosα，n=$\sqrt{a}$sinα，x=$\sqrt{b}$cosβ，y=$\sqrt{b}$sinβ，将其代入mx+ny中，由三角函数公式和最值分析可得答案．

解答解：令m=$\sqrt{a}$cosα，n=$\sqrt{a}$sinα，x=$\sqrt{b}$cosβ，y=$\sqrt{b}$sinβ，
则mx+ny=$\sqrt{ab}$cosαcosβ+$\sqrt{ab}$sinαsinβ=$\sqrt{ab}$cos（α-β）≤$\sqrt{ab}$，
当cos（α-β）=1时，取得最大值$\sqrt{ab}$．
故选B．

点评本题主要考查求最值问题的解法，注意运用三角换元，注意利用基本不等式求最值的条件易忽略，属于中档题和易错题．

练习册系列答案

相关题目

10．

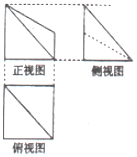已知某几何体的三视图如图所示，俯视图中正方形的边长为2，正视图中直角梯形的两底长为1和2，则此几何体的体积为（　　）

8．A，B，C是球O上的三点，AB=5，AC=3，BC=4，球O的直径等于13，则球心O到平面ABC的距离为（　　）

15．已知函数f（x）=${log_{\frac{1}{2}}}|{sin（x-\frac{π}{4}）}$|．
（1）求函数f（x）的定义域和值域；
（2）判定f（x）的奇偶性，并求出它的单调区间．

5．已知椭圆C₁：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的左、右两个焦点分别为F₁、F₂，离心率为$\frac{1}{2}$，且抛物线C₂：y²=4mx（m＞0）与椭圆C₁有公共焦点F₂（1，0）．
（1）求椭圆和抛物线的方程；
（2）设A、B为椭圆上的两个动点，$\overrightarrow{OA}•\overrightarrow{OB}$=0，过原点O作直线AB的垂线OD，垂足为D，求点D为轨迹方程．

12．下列四个选项错误的是（　　）

	A．	命题“若x≠1，则x²-3x+2≠0”的逆否命题是“若x²-3x+2=0，则x=1”
	B．	若p∨（￢q）为假命题，则p∧q为假命题
	C．	“a≠5且b≠-5”是“a+b≠0”的充分不必要条件
	D．	若命题p：?x∈R，x²+x+1≠0，则￢p：?x₀∈R，${x_0}^2+{x_0}+1=0$

9．记椭圆$\frac{x^2}{4}+\frac{{n{y^2}}}{4n+1}$=1围成的区域（含边界）为Ω_n（n=1，2，3…），当点（x，y）分别在Ω₁，Ω₂，…上时，x+y的最大值分别是M₁，M₂，…，则$\lim_{n→+∞}{M_n}$=2$\sqrt{2}$．

10．已知平行于x轴的直线分别交曲线y=e^2x+1与y=$\sqrt{2x-1}$于A，B两点，则|AB|的最小值为（　　）

试题分类