题目内容
2mx-my+x-y-3=0恒过点 ．
考点：恒过定点的直线
专题：直线与圆
分析：把原直线方程含有m的式子提取m，然后联立两直线
，求得交点得答案．
|
解答：
解：由2mx-my+x-y-3=0，得m（2x-y）+x-y+3=0．
由
，解得
．
∴2mx-my+x-y-3=0恒过点（3，6）．
故答案为：（3，6）．
由
|
|
∴2mx-my+x-y-3=0恒过点（3，6）．
故答案为：（3，6）．
点评：本题考查了恒过定点的直线，考查了直线系方程，是基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
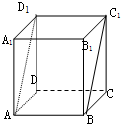如图，正方体ABCD-A1B1C1D1中，平面ABC1D1与平面ABCD所成二面角的大小为（ ）| A、300 |
| B、450 |
| C、600 |
| D、900 |
已知正项等比数列{an}满足S3-3a1-2a2=0，若存在两项an•am使得
=4a1，则
+
的最小值是（ ）
| aman |
| 1 |
| m |
| 4 |
| n |
| A、9 | ||
B、
| ||
C、
| ||
D、
|
若向量
，
，
的起点M和终点A，B，C互不重合，且无三点共线，则能使向量
，
，
成为空间一个基底的关系式是（ ）
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
已知 PH⊥Rt△HEF所在的平面，且HE⊥EF，连接PE，PF，则图中直角三角形的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |