题目内容
已知F1、F2为椭圆C:
+
=1的左、右焦点,则在该椭圆上能够满足∠F1PF2=90°的点P共有 个.
| x2 |
| 9 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由椭圆方程求得椭圆的长半轴长及离心率,设出P的坐标,由焦半径公式得到左右焦半径,结合勾股定理求得P的坐标得答案.
解答:
解:设P(x0,y0)为椭圆
+
=1上的一点,
由a2=9,b2=4,得c2=a2-b2=5,c=
.
∴2c=2
.
由焦半径公式得:|PF1|=3+
x0,|PF2|=3-
x0,
若∠F1PF2=90°,
则(3+
x0)2+(3-
x0)2=(2
)2,解得:x0=±
.
∴椭圆上能够满足∠F1PF2=90°的点P共有4个.
故答案为:4.
| x2 |
| 9 |
| y2 |
| 4 |
由a2=9,b2=4,得c2=a2-b2=5,c=
| 5 |
∴2c=2
| 5 |
由焦半径公式得:|PF1|=3+
| ||
| 3 |
| ||
| 3 |
若∠F1PF2=90°,
则(3+
| ||
| 3 |
| ||
| 3 |
| 5 |
3
| ||
| 5 |
∴椭圆上能够满足∠F1PF2=90°的点P共有4个.
故答案为:4.
点评:本题考查了椭圆的简单几何性质,考查了焦半径公式的运用,是基础题.

练习册系列答案
相关题目
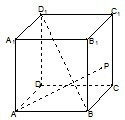 如图,正方体ABCD-A1B1C1D1的棱长为1,点P在侧面CBB1C1及其边界上运动,并且总保持B1P∥平面A1BD,则动点P的轨迹的长度是
如图,正方体ABCD-A1B1C1D1的棱长为1,点P在侧面CBB1C1及其边界上运动,并且总保持B1P∥平面A1BD,则动点P的轨迹的长度是 如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.