题目内容

3．抛物线x2=-$\frac{1}{2}$y的准线方程是（　　）
A．x=$\frac{1}{2}$B．x=$\frac{1}{8}$C．y=$\frac{1}{2}$D．y=$\frac{1}{8}$

分析 直接利用抛物线的标准方程求解P，然后求出准线方程．

解答 解：抛物线x2=-$\frac{1}{2}$y，可得p=$\frac{1}{4}$，
抛物线x2=-$\frac{1}{2}$y的准线方程是：y=$\frac{1}{8}$．
故选：D．

点评 本题考查抛物线的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
13．计算：$\sqrt{（{lo{g}_{2}5）}^{2}-4lo{g}_{2}5+4}$+log2$\frac{1}{5}$．
14．直线l过定点（-1，2）且在两坐标轴上的截距相等，则直线l的方程为（　　）
A．2x+y=0或x+y-1=0B．2x-y=0或x+y-1=0
C．2x+y=0或x-y+3=0D．x+y-1=0或x-y+3=0
11．命题“?x∈R，x2-2x+4≥0”的否定为?x∈R，x2-2x+4＜0．
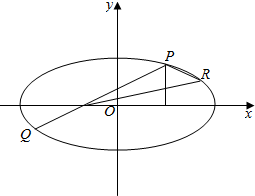18．如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的焦点为F1、F2，过F2作垂直于x轴的直线交椭圆于P点（点P在x轴上方），连结PF1并延长交椭圆于另一点Q．设$\overrightarrow{P{F_1}}=λ\overrightarrow{{F_1}Q}$（2≤λ≤$\frac{7}{3}$）．
（1）若PF1=$\frac{6}{5}\sqrt{5}$，PF2=$\frac{4}{5}\sqrt{5}$，求椭圆的方程；
（2）求椭圆的离心率的范围；
（3）当离心率最大时，过点P作直线l交椭圆于点R，设直线PQ的斜率为k1，直线RF1的斜率为k2，若k1=$\frac{3}{2}{k_2}$，求直线l的斜率k．
8．已知Pn（xn，yn）（n=1，2，3，…）是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1右支上的一点，F1、F2为双曲线的左右焦点，且满足P1F2⊥F1F2，|Pn+1F2|=|PnF1|，则|P25F2|的值为$\frac{71}{2}$．
15．阅读算法流程图，运行相应的程序，输出的结果为$\frac{5}{3}$
12．已知抛物线的顶点在坐标原点，焦点是圆（x-3）2+y2=4的圆心，则抛物线的方程是（　　）
A．x2=12yB．x2=6yC．y2=12xD．y2=6x
13．圆心在原点，半径为4的圆的方程为x2+y2=16．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网