题目内容
19.设a,b,c是三条不同的直线,α,β,γ是三个不同的平面,已知α∩β=a,α∩γ=b,β∩γ=c,下列四个命题中不一定成立的是( )| A. | 若a、b相交,则a、b、c三线共点 | B. | 若a、b平行,则a、b、c两两平行 | ||
| C. | 若a、b垂直,则a、b、c两两垂直 | D. | 若α⊥γ,β⊥γ,则a⊥γ |
分析 A.根据空间点与直线和平面的关系判断.B.利用直线平行的性质和判定定理判断.C.根据空间点与直线和平面的关系判断.D.根据面面垂直的位置关系判断.
解答  解:A.设a∩b=P,则P∈a.P∈b,又α∩β=a,α∩γ=b,∴P∈β.P∈γ,∵α∩γ=c,∴P∈c,即a、b、c三线共点,则A正确.
解:A.设a∩b=P,则P∈a.P∈b,又α∩β=a,α∩γ=b,∴P∈β.P∈γ,∵α∩γ=c,∴P∈c,即a、b、c三线共点,则A正确.
B.若a∥b,因为α∩γ=b,∴a∥β,a∥γ,因为α∩β=a,β∩γ=c,∴a∥c,∴a∥b∥c,故B正确.
C.如图,若a⊥b,则a不一定垂直c,b不一定垂直c,故C不一定正确.
D.若α⊥γ,β⊥γ,则a⊥c,a⊥b,∵a∩b=c,∴a⊥γ故D成立,
故选:C.
点评 本题主要考查空间直线与平面的位置关系的判断,利用平面的性质和定理是解决本题的关键.

练习册系列答案
相关题目
9.某品牌汽车4S点,对该品牌旗下的A型、B型、C型汽车进行维修保养调查,汽车4S店记录了该品牌三种类型汽车的维修情况,整理得下表:
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(Ⅰ)求A型,B型,C型各车型汽车的数目;
(Ⅱ)从抽取的A型和B型汽车中随机再选出2辆汽车进行电话回访,求这2辆汽车来自同一类型的概率;
(Ⅲ)维修结束后这100辆汽车的司机采用“100分制”“打分的方式表示4S店的满意度,按照大于等于80优秀,小于80合格,得到如下列联表
问:能否在犯错误概率不超过0.01前提下认为司机对4S店满意度调查于性别有关?请说明原因.
附
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 40 | 40 |
(Ⅰ)求A型,B型,C型各车型汽车的数目;
(Ⅱ)从抽取的A型和B型汽车中随机再选出2辆汽车进行电话回访,求这2辆汽车来自同一类型的概率;
(Ⅲ)维修结束后这100辆汽车的司机采用“100分制”“打分的方式表示4S店的满意度,按照大于等于80优秀,小于80合格,得到如下列联表
| 优秀 | 合格 | 不合格 | |
| 男司机 | 10 | 38 | 48 |
| 女司机 | 25 | 27 | 52 |
| 合计 | 35 | 65 | 100 |
附
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
10.《张丘建算经》是我国北魏时期大数学家丘建所著,约成书于公元466-485年间.其中记载着这么一道题:某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天共织布390尺,则该女子织布每天增加的尺数(不作近似计算)为( )
| A. | $\frac{16}{29}$ | B. | $\frac{16}{27}$ | C. | $\frac{11}{13}$ | D. | $\frac{13}{29}$ |
8.通过市场调查知某商品每件的市场价y(单位:圆)与上市时间x(单位:天)的数据如下:
根据上表数据,当a≠0时,下列函数:①y=ax+k;②y=ax2+bx+c;③y=alogmx中能恰当的描述该商品的市场价y与上市时间x的变化关系的是(只需写出序号即可)②.
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
9.过点M(1,4)与两条坐标轴围成的三角形面积等于1的所在直线方程是( )
| A. | 2x-y+2=0 | B. | 3x-y+1=0 | ||
| C. | 8x-y-4=0 | D. | 2x-y+2=0或8x-y-4=0 |
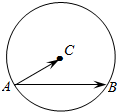 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.