题目内容
若f(x)=a+bsinx(b<0)的最大值为
,最小值为-
,求:
(1)f(x)的解析式;
(2)在区间(0,2π)内使f(x)=0的x值.
| 3 |
| 2 |
| 1 |
| 2 |
(1)f(x)的解析式;
(2)在区间(0,2π)内使f(x)=0的x值.
考点:三角函数的最值,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据函数的最值性质,建立方程组求出a,b即可f(x)的解析式;
(2)根据函数f(x)的解析式,解方程即可.
(2)根据函数f(x)的解析式,解方程即可.
解答:
解:(1)∵b<0,
∴当sinx=1时,函数取得最小值,当sinx=-1时,函数取得最大值,
即
,解得a=
,b=-1,
即f(x)=
-sinx.
(2)由f(x)=
-sinx=0得sinx=
,
则区间(0,2π)内,x=
或
.
∴当sinx=1时,函数取得最小值,当sinx=-1时,函数取得最大值,
即
|
| 1 |
| 2 |
即f(x)=
| 1 |
| 2 |
(2)由f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
则区间(0,2π)内,x=
| π |
| 6 |
| 5π |
| 6 |
点评:本题主要考查三角函数解析式的求解,根据三角函数的最值性质建立方程组是解决本题的关键.

练习册系列答案
相关题目
若i为虚数单位,则i+i2+i3+i4的值为( )
| A、-1 | B、i | C、0 | D、1 |
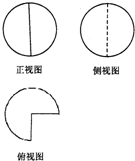 一个半径为1的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为( )
一个半径为1的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为( )| A、16π | ||
| B、14π | ||
| C、4π | ||
D、
|
已知O是△ABC所在平面上的一点,若
=
(其中P是ABC所在平面内任意一点),则O点是△ABC的( )
| PO |
a
| ||||||
| a+b+c |
| A、外心 | B、内心 | C、重心 | D、垂心 |