题目内容

已知集合A={x|
x-3
1-x
＞0}，函数y=log
1
2
（2-x2）的定义域为集合B，则A∩B=
 
．
考点：交集及其运算
专题：集合
分析：根据条件求出对应的集合A，B，即可得到结论．
解答： 解：由
x-3
1-x
＞0得（x-3）（x-1）＜0，即1＜x＜3，则A=（1，3），
由2-x2＞0，解得-
2
＜x＜
2
，即B=（-
2
，
2
），
则A∩B=（1，
2
），
故答案为：（1，
2
）
点评：本题主要考查集合的基本运算，根据条件求出集合A，B是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x）=3lnx-
1
2
x2+2x．
（1）确定函数f（x）的单调区间，并指出其单调性；
（2）求函数y=f（x）的图象在点x=1处的切线与两坐标轴所围成的三角形的面积．
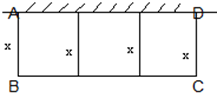有一批材料可以建成长为200m的围墙，如果用材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的矩形（如图），求：
①整个矩形场地ABCD的面积S用x表示出来；
②当中间隔墙x为多少时，整个矩形场地ABCD的S最大面积是多少？
角θ（0＜θ＜π）的正弦线与余弦线的长度相等且符号相反，则θ的值为
 
．
动点P在边长为1的正方形ABCD内运动，则动点P到顶点A的距离|PA|≤1的概率为
 
．
直线y=-x+b与5x+3y-31=0的交点在第一象限，则b的取值范围是
 
．
抛物线y2=2px（p＞0）上一点P到焦点F的距离为2p，则点P的坐标为
 
．
若数列{an}、{bn}的通项公式分别是an=（-1）n+2007•a，bn=2+
(-1)n+2008
n
，且an＜bn，对任意n∈N*恒成立，则常数a的取值范围是
 
．
已知空间三点A（-2，0，2），B（-1，1，2），C（-3，0，4），设
a
=
AB
，
b
=
AC
，若向量k
a
+
b
与k
a
-2
b
互相垂直，则k的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网