题目内容
17.设函数$f(x)=\sqrt{3}sinx+cosx,x∈[{0,2π}]$,若0<a<1,则方程f(x)=a的所有根之和为( )| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | 3π |
分析 先进行化简函数f(x),利用三角函数的对称性进行求解即可.
解答 解:由辅助角公式得$f(x)=2sin({x+\frac{π}{6}})$,
∵x∈[0,2π],∴f(x)∈[-2,2],
∵0<a<1,∴方程f(x)=α有两根x1,x2,
由对称性,有$\frac{{({{x_1}+\frac{π}{6}})+({{x_2}+\frac{π}{6}})}}{2}=\frac{3π}{2}$,
∴${x_1}+{x_2}=\frac{8π}{3}$,
故选:C.
点评 本题主要考查三角函数根的求解和应用,利用辅助角公式结合三角函数的对称性是解决本题的关键,综合性较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数y=ax3+bx2+cx+d的图象如图所示,则( )


| A. | a>0,b>0,c>0 | B. | a>0,b>0,c<0 | C. | a<0,b<0,c>0 | D. | a<0,b<0,c<0 |
8.不透明袋子中放有大小相同的5个球,球上分别标有号码1,2,3,4,5,若从袋中任取三个球,则这三个球号码之和为5的倍数的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{4}$ |
5.执行如图所示的程序框图,如果输入x=3,则输出k的值为( )


| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
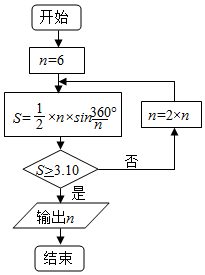 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( ) 已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.
已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.