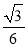题目内容
14.函数y=ax3+bx2+cx+d的图象如图所示,则( )
| A. | a>0,b>0,c>0 | B. | a>0,b>0,c<0 | C. | a<0,b<0,c>0 | D. | a<0,b<0,c<0 |
分析 求导y′=3ax2+2bx+c,结合图象可得二次函数y′=3ax2+2bx+c的图象开口向上,且3ax2+2bx+c=0有一正一负两个不同的根,从而解得.
解答 解:∵y=ax3+bx2+cx+d,
∴y′=3ax2+2bx+c,
∵函数y=ax3+bx2+cx+d从左到右先增后减后增,
∴二次函数y′=3ax2+2bx+c的图象开口向上,
∴a>0,
∴排除C、D;
∵函数y=ax3+bx2+cx+d的极值点一正一负,
∴3ax2+2bx+c=0有一正一负两个不同的根,
∴$\frac{c}{3a}$<0,
∴c<0,
故排除A,
故选B.
点评 本题考查了导数在判断函数的单调性与极值时的应用,同时考查了二次函数的性质应用及数形结合的思想应用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
9.已知a>0,b>0,则“ab>1”是“a+b>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
16.某毕业班统计全班40名学生报名参加学科竞赛和报名参加自主招生的数据如表:
(1)从该班随机选1名同学,求该同学仅报名参加其中一项的概率;
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
| 报名参加学科竞赛 | 未报名参加学科竞赛 | |
| 报名参加自主招生 | 2 | 4 |
| 未报名参加自主招生 | 6 | 28 |
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
17.设函数$f(x)=\sqrt{3}sinx+cosx,x∈[{0,2π}]$,若0<a<1,则方程f(x)=a的所有根之和为( )
| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | 3π |
 与圆
与圆 的位置关系为( )
的位置关系为( )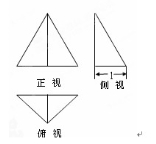
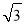 B.
B.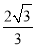 C.
C.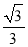 D.
D.