题目内容
8.不透明袋子中放有大小相同的5个球,球上分别标有号码1,2,3,4,5,若从袋中任取三个球,则这三个球号码之和为5的倍数的概率为( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{4}$ |
分析 用列举法求出从分别标有号码1,2,3,4,5的袋中任取三个球的基本事件数,计算所求的概率即可.
解答 解:从分别标有号码1,2,3,4,5的袋中任取三个球,基本事件数是
(1、2、3),(1、2、4),(1、2、5),(1、3、4),(1、3、5),(1、4、5),
(2、3、4),(2、3、5),(2、4、5),(3、4、5)共10种;
其中这三个球号码之和为5的倍数的事件为(1、4、5),(2、3、5)共2种;
所以,所求的概率为P=$\frac{2}{10}$=$\frac{1}{5}$.
故选:B.
点评 本题考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
16.某毕业班统计全班40名学生报名参加学科竞赛和报名参加自主招生的数据如表:
(1)从该班随机选1名同学,求该同学仅报名参加其中一项的概率;
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
| 报名参加学科竞赛 | 未报名参加学科竞赛 | |
| 报名参加自主招生 | 2 | 4 |
| 未报名参加自主招生 | 6 | 28 |
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
17.设函数$f(x)=\sqrt{3}sinx+cosx,x∈[{0,2π}]$,若0<a<1,则方程f(x)=a的所有根之和为( )
| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | 3π |
 B.
B.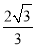 C.
C.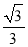 D.
D.