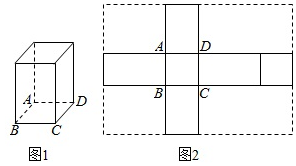
题目内容
9.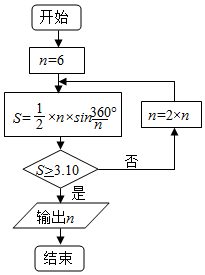 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
分析 列出循环过程中S与n的数值,满足判断框的条件即可结束循环.
解答 解:模拟执行程序,可得:
n=6,S=3sin60°=$\frac{3\sqrt{3}}{2}$,
不满足条件S≥3.10,n=12,S=6×sin30°=3,
不满足条件S≥3.10,n=24,S=12×sin15°=12×0.2588=3.1056,
满足条件S≥3.10,退出循环,输出n的值为24.
故选:B.
点评 本题考查循环框图的应用,考查了计算能力,注意判断框的条件的应用,属于基础题.

练习册系列答案
相关题目
17.设函数$f(x)=\sqrt{3}sinx+cosx,x∈[{0,2π}]$,若0<a<1,则方程f(x)=a的所有根之和为( )
| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | 3π |
4.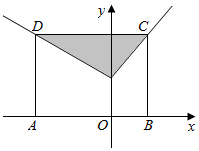 如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
 如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
14.已知复数z满足$\frac{2z+m}{z-3}=i$,且z的实部与虚部之和为0,则实数m等于( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
1.在直角坐标平面上,已知点A(0,2),B(0,1),D(t,0)(t>0),M为线段AD上的动点,若|AM|≤2|BM|恒成立,则实数t的取值范围为( )
| A. | $[\frac{{2\sqrt{3}}}{3},+∞)$ | B. | $[\frac{{\sqrt{3}}}{3},+∞)$ | C. | $(0,\frac{{2\sqrt{3}}}{3}]$ | D. | $(0,\frac{4}{3})$ |
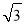 B.
B.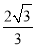 C.
C.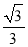 D.
D.