题目内容
将一颗骰子先后抛掷两次，观察向上的点数．则点数相同的概率是 ．
考点：古典概型及其概率计算公式
专题：计算题,概率与统计
分析：列举出所有情况，让出现相同点数的情况数除以总情况数即为所求的概率．
解答：
解：同时抛掷两枚骰子，出现点数情况共有6×6=36种情况如下表．
点数相同的有6种，即（1，1），（2，2），（3，3），（4，4），（5，5），（6，6），
点数相同的概率为
=
．
故答案为：
．
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | 1，6（ ） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （35） | （3，6） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| 6 | （6，1） | （6，2） | （6，3） | （64） | （6，5） | （6，6） |
点数相同的概率为
| 6 |
| 36 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
．
| m |
| n |
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
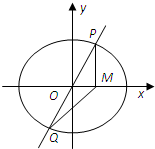已知椭圆C的两焦点F1（-1，0）、F2（1，0），离心率为
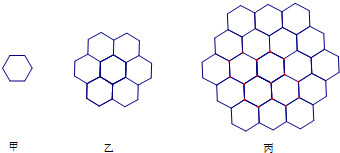如图，一组蜂巢的截面图，其中第一个图甲有一个蜂巢，第二个图乙有7个蜂巢，第三个图丙有19个蜂巢，按此规律，以f（n）表示第n个图蜂巢总数，则f（4）=已知x∈R，则“x2-3x＜0”是“（x-1）（x-2）≤0成立”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |