题目内容
17.已知一个质点在腰长为4的等腰直角三角形内随机运动,则某时刻该质点距离三角形的三个顶点的距离均超过1的概率为1-$\frac{π}{16}$.分析 根据几何概型的概率公式求出对应区域的面积,进行求解即可
解答  解:若质点P到三个顶点的距离都超过1,
解:若质点P到三个顶点的距离都超过1,
则P的位置位于阴影部分如图
三角形在三个圆的面积之和为$\frac{1}{2}$×π×12=$\frac{π}{2}$,
△ABC的面积S=$\frac{1}{2}$×4×4=8,
则阴影部分的面积S=8-$\frac{π}{2}$,
则对应的概率P=$\frac{8-\frac{π}{2}}{8}=1-\frac{π}{16}$;
故答案为:$1-\frac{π}{16}$,
点评 本题主要考查几何概型的概率的计算,根据条件求出阴影部分的面积是解决本题的关键.

练习册系列答案
相关题目
8.等差数列3,1,-1,-3,…,-93的项数为( )
| A. | 52 | B. | 51 | C. | 49 | D. | 50 |
12.已知正方形ABCD的对角线相交于点O,若随机向此正方形内投放一颗豆子,则它落在△AOB内的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
9.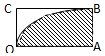 如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
 如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
6.设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
7.将函数f(x)=2sin2x的图象向左平移$\frac{π}{12}$个单位后得到函数g(x)的图象,若函数g(x)在区间[0,$\frac{a}{3}$]和[2a,$\frac{7π}{6}$]上均单调递增,则实数a的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$] | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | [$\frac{π}{4}$,$\frac{3π}{8}$] |
 某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有3•2n-3条线段.
某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有3•2n-3条线段.