题目内容
已知平面向量
,
,满足
=(1,
),|
|=3,
⊥(
-2
),则|
-
|=( )
| a |
| b |
| a |
| 3 |
| b |
| a |
| a |
| b |
| a |
| b |
| A、2 | B、3 | C、4 | D、6 |
考点:数量积判断两个平面向量的垂直关系,向量的模
专题:平面向量及应用
分析:由题意易得|
|=2,|
|2-2
•
=0,代入可得|
-
|2=|
|2-2
•
+|
|2=9,开平方可得.
| a |
| a |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
解答:
解:∵
=(1,
),∴|
|=2,
又∵|
|=3,
⊥(
-2
),
∴
•(
-2
)=|
|2-2
•
=0,
∴|
-
|2=|
|2-2
•
+|
|2=0+9=9,
∴|
-
|=3.
故选:B.
| a |
| 3 |
| a |
又∵|
| b |
| a |
| a |
| b |
∴
| a |
| a |
| b |
| a |
| a |
| b |
∴|
| a |
| b |
| a |
| a |
| b |
| b |
∴|
| a |
| b |
故选:B.
点评:本题考查平面向量的数量积和垂直关系,涉及向量的模长公式,属基础题.

练习册系列答案
相关题目
实数x、y满足x2+2xy+y2+x2y2=1,则x-y的最大值为( )
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
如图所示,AC1是正方体的一条体对角线,点P,Q分别为其在棱的中点,则PQ与AC1所成的角为( ) 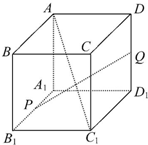

A、
| ||
B、
| ||
C、
| ||
D、
|