题目内容
3.设A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A⊆B的B的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由题意可知:集合B中至少含有元素1,2,即可得出.
解答 解:A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A⊆B的B为:{1,2},{1,2,3},{1,2,4},{1,2,3,4}.
故选:B.
点评 本题考查了集合之间的运算性质、元素与集合之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.定义:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,若复数z满足$|\begin{array}{l}{z}&{1}\\{i}&{-i}\end{array}|$=-1-i,则z等于( )
| A. | 1+i | B. | 1-i | C. | -i | D. | 3-i |
8.复数z=$\frac{2i}{1+i}$的共轭复数是( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
13.已知不等式组$\left\{\begin{array}{l}3x+4y-10≥0\\ x≤4\\ y≤3\end{array}\right.$表示区域D,过区域D中任意一点P作圆x2+y2=1的两条切线且切点分别为A,B,当∠PAB最小时,cos∠PAB=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{1}{2}$ |
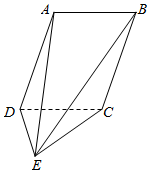 如图,平行四边形ABCD⊥平面CDE,AD⊥DE.
如图,平行四边形ABCD⊥平面CDE,AD⊥DE.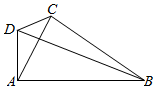 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.