题目内容
15.已知△ABC的顶点A(-1,-1)、B(3,2)、C(1,4),求BC边的中线的长度.分析 先求出BC的中点坐标,再利用两点间距离公式能求出BC边的中线的长度.
解答 解:∵△ABC的顶点A(-1,-1)、B(3,2)、C(1,4),
∴BC的中点D(2,3),
∴BC边的中线的长度|AD|=$\sqrt{(2+1)^{2}+(3+1)^{2}}$=5.
∴BC边的中线的长度为5.
点评 本题考查中线长度的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在△ABC中,若tanA,tanB,tanC均为整数,且∠A>∠B>∠C,则下列选项错误( )
| A. | ∠A<80° | B. | ∠B<60° | C. | ∠C<50° | D. | ∠A>65° |
10.已知集合A={x|x2-4x<0},B={x|-1≤x≤1},则A∪B=( )
| A. | [-1,1] | B. | [-1,4) | C. | (0,1] | D. | (0,4) |
20.某单位有职工200人,其年龄分布如下表:
为了解该单位职工的身体健康状况,用分层抽样的方法抽取一个容量为40的样本进行调查,则年龄在[30,40]内的职工应抽取的人数为18.
| 年龄(岁) | [20,30] | [30,40] | [40,60] |
| 人数 | 70 | 90 | 40 |
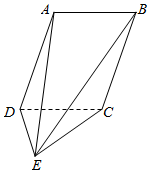 如图,平行四边形ABCD⊥平面CDE,AD⊥DE.
如图,平行四边形ABCD⊥平面CDE,AD⊥DE.