题目内容
17.在正三棱锥V-ABC中,底面边长为3,三棱锥的高是3,D是VC的中点,则异面直线BD和VA所成角的余弦值是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{10}}{8}$ | D. | $\frac{\sqrt{10}}{5}$ |
分析 建立空间坐标系,代入点的坐标,求出$\overrightarrow{BD},\overrightarrow{VA}$的夹角即可.
解答 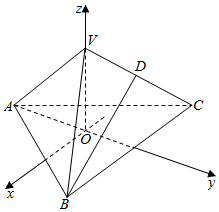 解:设底面ABC的中心为O,以O为坐标原点建立如图所示的空间坐标系O-xyz,
解:设底面ABC的中心为O,以O为坐标原点建立如图所示的空间坐标系O-xyz,
∵棱锥的底面边长为3,高为3,
∴A(0,-$\sqrt{3}$,0),B($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0),C(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0),V(0,0,3).
∴D(-$\frac{3}{4}$,$\frac{\sqrt{3}}{4}$,$\frac{3}{2}$).
∴$\overrightarrow{BD}$=(-$\frac{9}{4}$,-$\frac{\sqrt{3}}{4}$,$\frac{3}{2}$),$\overrightarrow{VA}$=(0,-$\sqrt{3}$,-3).
∴|$\overrightarrow{BD}$|=$\frac{\sqrt{30}}{2}$,|$\overrightarrow{VA}$|=2$\sqrt{3}$.$\overrightarrow{BD}•\overrightarrow{VA}$=-$\frac{15}{4}$.
∴cos<$\overrightarrow{BD}$,$\overrightarrow{VA}$>=$\frac{\overrightarrow{BD}•\overrightarrow{VA}}{|\overrightarrow{BD}||\overrightarrow{VA}|}$=-$\frac{\sqrt{10}}{8}$.
∴异面直线BD和VA所成角的余弦值是$\frac{\sqrt{10}}{8}$.
故选:C.
点评 本题考查了空间角的计算,向量法是常用的解决空间角的方法之一.

| A. | (0,$\frac{15}{16}$) | B. | ($\frac{15}{16}$,1) | C. | (1,$\frac{16}{15}$) | D. | (1,$\frac{5}{4}$) |
| A. | ∠A<80° | B. | ∠B<60° | C. | ∠C<50° | D. | ∠A>65° |
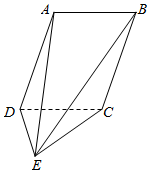 如图,平行四边形ABCD⊥平面CDE,AD⊥DE.
如图,平行四边形ABCD⊥平面CDE,AD⊥DE.