题目内容
8.函数f(x)=4sin($\frac{1}{2}$x+$\frac{π}{6}$)的最小正周期是( )| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 根据正弦函数的y=Asin(ωx+φ)的形式的周期公式求函数的最小正周期即可.
解答 解:函数f(x)=4sin($\frac{1}{2}$x+$\frac{π}{6}$),
其最小正周期T=$\frac{2π}{|ω|}=\frac{2π}{\frac{1}{2}}=4π$,
故选:D.
点评 本题考查了三角函数的y=Asin(ωx+φ)的形式的周期公式的运用.比较基础.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
19.在五张牌中有三张K和两张A,如果不放回地一次抽取两张牌.记“第2次抽到扑克牌K的概率为x”,“在第一次抽到扑克牌K的条件下,第二次抽到扑克牌K的概率为y”,则实数x,y依次为( )
| A. | $\frac{3}{5}{,^{\;}}\frac{1}{2}$ | B. | $\frac{3}{5}{,^{\;}}\frac{3}{5}$ | C. | $\frac{1}{2}{,^{\;}}\frac{1}{2}$ | D. | $\frac{3}{5}{,^{\;}}\frac{2}{5}$ |
3.把正奇数从小到大按以下方式分钟:(1),(3,5),(7,9,11),(13,15,17,19),…,其中第n组有n个正奇数,若第m组第k个正奇数是 2015,则m+k=( )
| A. | 63 | B. | 64 | C. | 65 | D. | 66 |
13.已知f(x)=x3-$\frac{9}{2}$x2+6x-a,若对任意的x,f′(x)≥m恒成立,则m的最大值为( )
| A. | 3 | B. | 2 | C. | 1 | D. | -$\frac{3}{4}$ |
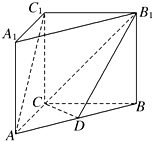 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.