题目内容
3.把正奇数从小到大按以下方式分钟:(1),(3,5),(7,9,11),(13,15,17,19),…,其中第n组有n个正奇数,若第m组第k个正奇数是 2015,则m+k=( )| A. | 63 | B. | 64 | C. | 65 | D. | 66 |
分析 由题意和等差数列的前n项和公式,求出前n组数中正奇数的个数是$\frac{1}{2}$n(n+1),再判断出2015是第1008个奇数,再由条件和特值法判断出2015应是第45组数的一个数,进而得到答案.
解答 解:由题意知,前n组数中正奇数的总个数是:1+2+3+…+n=$\frac{1}{2}$n(n+1),
因为2015=2×1008-1,故2015是第1008个奇数,
而$\frac{1}{2}$×44×45=990<1008,$\frac{1}{2}$×45×46=1035>1008,
所以第44组中的最大数是第990个奇数,
以第45组中的最大数是第1035个奇数,
故第1008个奇数:2015应是45组的第18个数,
故m=45,k=18,
故m+k=63
故选:A
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.已知函数y=sin(2x-$\frac{π}{6}$)-m在[$\frac{π}{2}$,π]上有两个零点,则m的取值范围为( )
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
8.函数f(x)=4sin($\frac{1}{2}$x+$\frac{π}{6}$)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
15. 如果执行如图所示的程序框图,则输出的结果为( )
如果执行如图所示的程序框图,则输出的结果为( )
 如果执行如图所示的程序框图,则输出的结果为( )
如果执行如图所示的程序框图,则输出的结果为( )| A. | 5 | B. | 7 | C. | 8 | D. | 13 |
12.定义在(0,+∞)上的单调递减函数f(x),若f(x)的导函数存在且满足$\frac{f(x)}{f'(x)}>-x$,则下列不等式成立的是( )
| A. | 3f(2)<2f(3) | B. | 3f(4)<4f(3) | C. | $\frac{f(3)}{4}>\frac{f(4)}{3}$ | D. | f(2)<2f(1) |
13.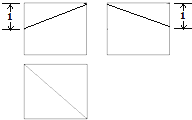 一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
 一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )| A. | $\frac{22}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 4 |