题目内容
已知函数f(x)=2sinωxcosωx=2
sin2ωx-
(ω>0)的最小正周期为π.
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移
个单位,再向上平移a(a>0)个单位,得到函数y=g(x)的图象.若y=g(x)在区间[0,
]上的最大值与最小值的和为5,求a的值.
| 3 |
| 3 |
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移
| π |
| 3 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)利用二倍角公式和两角和公式对函数解析式化简整理,利用周期公式求得ω,则函数解析式可得,最后利用正弦函数单调性求得函数的单调增区间.
(Ⅱ)根据图象平移的法则求得函数g(x)的解析式,进而根据x的范围确定x+
的范围,进而根据三角函数的性质求得函数的最大和最小值的表达式,进而求得a.
(Ⅱ)根据图象平移的法则求得函数g(x)的解析式,进而根据x的范围确定x+
| π |
| 3 |
解答:
解:(Ⅰ)由题意得f(x)=2sinωxcosωx+2
sin2ωx-
=sin2ωx-
cos2ωx=2sin(2ωx-
)
由周期为π,得ω=
=1.
得F(X)=2sin(2x-
),
由2kπ-
≤2x-
≤2kπ+
,得kπ-
≤x≤kπ+
,k∈Z
所以函数f(x)的单调增区间是[kπ-
,kπ+
],k∈Z.
(Ⅱ)将函数f(x)的图象向左平移
个单位,再向上平移a个单位,
得到g(x)=2sin(2x+
)+a,
因为x∈[0,
],2x+
∈[
,
],sin(2x+
)∈[
,1],
所以g(x)∈[1+a,2+a],
令1+a+2+a=5
得a=1
| 3 |
| 3 |
| 3 |
| π |
| 3 |
由周期为π,得ω=
| 2π |
| T |
得F(X)=2sin(2x-
| π |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
所以函数f(x)的单调增区间是[kπ-
| π |
| 12 |
| 5π |
| 12 |
(Ⅱ)将函数f(x)的图象向左平移
| π |
| 3 |
得到g(x)=2sin(2x+
| π |
| 3 |
因为x∈[0,
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
所以g(x)∈[1+a,2+a],
令1+a+2+a=5
得a=1
点评:本题主要考查了三角函数图象与性质,三角函数恒等变换的应用.综合性强,是这几年高考常考的题型.

练习册系列答案
相关题目
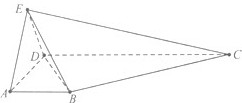 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=