题目内容
设等差数列{an}的前n项和为Sn,已知(a8-1)3+2015(a8-1)=1,(a2008-1)3+2015(a2008-1)=-1,则下列结论正确的是( )
| A、S2015=2015,a2008<a8 |
| B、S2015=2015,a2008>a8 |
| C、S2015=-2015,a2008≤a8 |
| D、S2015=-2015,a2008≥a8 |
考点:数列的函数特性
专题:函数的性质及应用,等差数列与等比数列
分析:构造函数f(x)=x3+2015x,判断奇偶性,单调性,得出f(x)是奇函数,a8+a2008=2,a8>a2008,即可判断答案.
解答:
解:设f(x)=x3+2015x,
∵f(-x)=-f(x),∴f(x)是奇函数,
∵f′(x)=3x2+2015>0,
∴f(x)=x3+2015x在R上单调递增,
∵(a8-1)3+2015(a8-1)=1,(a2008-1)3+2015(a2008-1)=-1
∴f(a8-1)=1,f(a2008-1)=-1,
∴a8>a2008,a8+a2008=2,
∵等差数列{an},
∴S2015=2015•
=2015
故选:A
∵f(-x)=-f(x),∴f(x)是奇函数,
∵f′(x)=3x2+2015>0,
∴f(x)=x3+2015x在R上单调递增,
∵(a8-1)3+2015(a8-1)=1,(a2008-1)3+2015(a2008-1)=-1
∴f(a8-1)=1,f(a2008-1)=-1,
∴a8>a2008,a8+a2008=2,
∵等差数列{an},
∴S2015=2015•
| (a1+a2015) |
| 2 |
故选:A
点评:本题考查了函数的性质在数列中的应用,属于中档题.

练习册系列答案
相关题目
已知x,y之间的几组数据如下表:
假设根据上表数据所得线性回归方程为y=b1x+a1,某同学根据上表中前两组数据求得的直线方程为y=b2x+a2,则以下结论正确的是( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
| A、b1>b2,a1>a2 |
| B、b1>b2,a1<a2 |
| C、b1<b2,a1>a2 |
| D、b1<b2,a1<a2 |
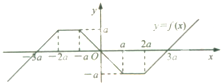 (理做)如图所示,函数y=f(x)的图象由两条射线和三条线段组成,若?x∈R,f(x)>f(x-2),则正实数的取值范围是
(理做)如图所示,函数y=f(x)的图象由两条射线和三条线段组成,若?x∈R,f(x)>f(x-2),则正实数的取值范围是