题目内容
3.已知椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的右焦点为F,P是椭圆上一点,点$A({0,2\sqrt{3}})$,当△APF的周长最大时,△APF的面积等于( )| A. | $\frac{{11\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{21}{4}$ |
分析 利用椭圆的定义,确定△APF周长最大时,P纵坐标,即可求出△APF周长最大时,该三角形的面积.
解答 解:椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的a=3,b=$\sqrt{5}$,c=$\sqrt{{a}^{2}-{b}^{2}}$=2,
由题意,设F′是左焦点,
则△APF周长=|AF|+|AP|+|PF|=|AF|+|AP|+2a-|PF′|=4+6+|PA|-|PF′|
≤10+|AF′|(A,P,F′三点共线时,且P在AF′的延长线上,取等号),
直线AF′的方程为$\frac{x}{-2}$+$\frac{y}{2\sqrt{3}}$=1与椭圆5x2+9y2=45,
联立可得32y2-20$\sqrt{3}$y-75=0,
解得P的纵坐标为-$\frac{5\sqrt{3}}{8}$,
则△APF周长最大时,
该三角形的面积为$\frac{1}{2}$|FF′|•|yA-yP|
=2•|2$\sqrt{3}$+$\frac{5\sqrt{3}}{8}$|=$\frac{21\sqrt{3}}{4}$.
故选:B.
点评 本题考查椭圆的定义,以及三点共线时取得最值,同时考查三角形面积的计算,确定P的坐标是关键.

练习册系列答案
相关题目
13.一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是( )
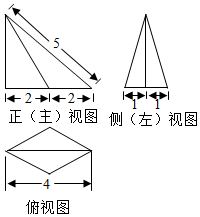

| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
14.“数列{an}成等比数列”是“数列{lgan+1}成等差数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布( )
| A. | 30尺 | B. | 90尺 | C. | 150尺 | D. | 180尺 |
8.已知函数f(x)=x3-x2-x+a的图象与x轴只有一个交点,则实数a的取值范围是( )
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
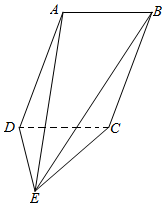 如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE
如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE