题目内容
过定点M(1,2)作两条相互垂直的直线l1、l2,设原点到直线l1、l2的距离分别为d1、d2,则d1+d2的最大值是 .
考点:点到直线的距离公式
专题:直线与圆
分析:由题意易得d12+d22=5,可设d1=
cosθ,d2=
sinθ,可得d1+d2=
sin(θ+φ),由三角函数的最值可得.
| 5 |
| 5 |
| 10 |
解答:
解:作OP⊥l1交l1于点P,作OQ⊥l2交l2于点Q,可得四边形OPMQ为矩形,
∴d12+d22=OM2=12+22=5,故可设d1=
cosθ,d2=
sinθ
∴d1+d2=
cosθ+
sinθ=
sin(θ+φ),其中tanφ=1,
∴当sin(θ+φ)取最大值1时,d1+d2=
sin(θ+φ)取最大值
故答案为:
∴d12+d22=OM2=12+22=5,故可设d1=
| 5 |
| 5 |
∴d1+d2=
| 5 |
| 5 |
| 10 |
∴当sin(θ+φ)取最大值1时,d1+d2=
| 10 |
| 10 |
故答案为:
| 10 |
点评:本题考查点到直线的距离,三角代换是解决问题的关键,属基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
给出下列四个命题,其中不正确的是( )
| A、函数y=tanx是增函数 | ||
B、y=|sin2x|的最小正周期是
| ||
C、函数y=cosx在[2kπ+π,2kπ+
| ||
D、函数y=tan(x+
|
 如图,在三棱锥A-BCD中,AB=CD=6,AC=BD=8,BC=10,且A在平面BCD上的投影O恰好在BD上.
如图,在三棱锥A-BCD中,AB=CD=6,AC=BD=8,BC=10,且A在平面BCD上的投影O恰好在BD上.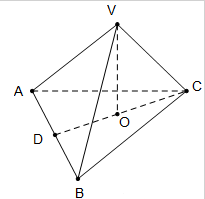 如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=
如图,三棱锥V-ABC中,VO⊥平面ABC,O∈CD,AB=4,AD=BD,VA=VB=