题目内容
已知f(3x+1)=
,则函数f(x)的解析式为 .
| 2x+1 |
| 3-4x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:令3x+1=t,则x=
(t-1),代入已知函数可得f(t),进而可得f(x)
| 1 |
| 3 |
解答:
解:令3x+1=t,则x=
(t-1),
代入已知函数可得f(t)=
=
,
∴f(x)=
故答案为:f(x)=
| 1 |
| 3 |
代入已知函数可得f(t)=
| ||
3-
|
| 2t+1 |
| 13-4t |
∴f(x)=
| 2x+1 |
| 13-4x |
故答案为:f(x)=
| 2x+1 |
| 13-4x |
点评:本题考查换元法求函数的解析式,属基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知双曲线C:
-
=1过点(2,3),且一条渐近线的倾斜角为
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)设双曲线C的左顶点为A1,右焦点为F2,P为双曲线C右支上一点,求
•
的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)设双曲线C的左顶点为A1,右焦点为F2,P为双曲线C右支上一点,求
| PA1 |
| PF2 |
数列{an}的前n项和为Sn,若an=
,则S7=( )
| 1 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
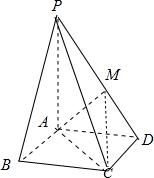 如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2
如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2 如图,在边长为2的正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,D1D,CD的中点,N是BC的中点,M在四边形EFGH上以及其内部运动,若MN∥平面A1BD,则M的轨迹的长度是( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,D1D,CD的中点,N是BC的中点,M在四边形EFGH上以及其内部运动,若MN∥平面A1BD,则M的轨迹的长度是( )