题目内容
设命题p:函数y=loga(x+1)(a>0,a≠1)在x∈(0,+∞)上单调递减;命题q:3x-9x<a对一切的x∈R恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:命题p:函数y=loga(x+1)(a>0,a≠1)在x∈(0,+∞)上单调递减,得出0<a<1,
命题q:3x-9x<a对一切的x∈R恒成立,得a>
,
p且q为真时,可得:
<a<1,最后可得出命题“p且q”为假命题时,实数a的取值范围.
命题q:3x-9x<a对一切的x∈R恒成立,得a>
| 1 |
| 4 |
p且q为真时,可得:
| 1 |
| 4 |
解答:
解:∵命题p:函数y=loga(x+1)(a>0,a≠1)在x∈(0,+∞)上单调递减,
∴x+1∈[1,+∞),0<a<1,
∵命题q:3x-9x<a对一切的x∈R恒成立,
∴f(x)=3x-(3x)2,
t=3x,y=-t2+t,t>0,
当t=
时,y的最大值
,
即必须得a>
,
∵p且q为真时,可得:
<a<1,
∴命题“p且q”为假命题时,实数a的取值范围为(0,
)∪(1,+∞),
∴x+1∈[1,+∞),0<a<1,
∵命题q:3x-9x<a对一切的x∈R恒成立,
∴f(x)=3x-(3x)2,
t=3x,y=-t2+t,t>0,
当t=
| 1 |
| 2 |
| 1 |
| 4 |
即必须得a>
| 1 |
| 4 |
∵p且q为真时,可得:
| 1 |
| 4 |
∴命题“p且q”为假命题时,实数a的取值范围为(0,
| 1 |
| 4 |
点评:本题综合考查了函数,不等式,简易逻辑等知识灵活运用,巧用对立事件求解.

练习册系列答案
相关题目
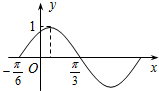 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
下列各式中正确的个数是( )
①0∈{0};②0∈∅;③∅?{0}④∅={0}.
①0∈{0};②0∈∅;③∅?{0}④∅={0}.
| A、1个 | B、2个 | C、3个 | D、4个 |
设a=log0.34,b=log0.30.2,c=(
)π( )
| 1 |
| e |
| A、a>b>c |
| B、b>c>a |
| C、b>a>c |
| D、c>b>a |