题目内容
20.已知函数y=f(x+1)是定义域为R的偶函数,且f(x)在[1,+∞)上单调递减,则不等式f(2x-1)>f(x+2)的解集为($\frac{1}{3}$,3).分析 根据y=f(x+1)是定义域为R的偶函数,得到y=f(x+1)的对称轴为y轴,进而确定出f(x)的对称轴,利用函数增减性求出所求不等式的解集即可.
解答 解:∵函数y=f(x+1)是定义域为R的偶函数,
∴y=f(x+1)关于y轴对称,
∴y=f(x)向左平移1个单位得到y=f(x+1),
∴y=f(x)关于直线x=1对称,
∵f(x)在[1,+∞)上单调递减,且f(2x-1)>f(x+2),
∴f(x)在(-∞,1]上单调递增,
∴|2x-1-1|<|x+2-1|,即(2x-2)2<(x+1)2,
整理得:3x2-10x+3<0,即(3x-1)(x-3)<0,
解得:$\frac{1}{3}$<x<3,
则不等式f(2x-1)>f(x+2)的解集为($\frac{1}{3}$,3).
故答案为:($\frac{1}{3}$,3)
点评 此题考查了奇偶性与单调性的综合,熟练掌握函数的奇偶性与单调性是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.$\frac{{2{{sin}^2}55°-1}}{sin20°}$的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -1 | D. | 1 |
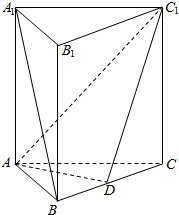 如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.