题目内容
甲船在早6点至12点之间的任意时刻出发,则它早于8点出发的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:确定件总数包含的时间长度是6,它早于8点出发的事件包含的时间长度是2,由几何概型公式得到结论.
解答:
解:由题意知这是一个几何概型,
∵甲船在早6点至12点之间的任意时刻出发,
∴事件总数包含的时间长度是6,
∵它早于8点出发的事件包含的时间长度是2,
由几何概型公式得到P=
=
,
故选:A.
∵甲船在早6点至12点之间的任意时刻出发,
∴事件总数包含的时间长度是6,
∵它早于8点出发的事件包含的时间长度是2,
由几何概型公式得到P=
| 2 |
| 6 |
| 1 |
| 3 |
故选:A.
点评:高中必修中学习了几何概型和古典概型两种概率问题,解题时,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.再看是不是几何概型,它的结果要通过长度、面积或体积之比来得到.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
变量y对x的回归方程的意义是( )
| A、表示y与x之间的函数关系 |
| B、表示y与x之间的线性关系 |
| C、反映y与x之间的真实关系 |
| D、反映y与x之间的真实关系达到最大限度的吻合 |
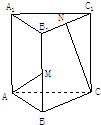 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列8,5,2,…的第20项是( )
| A、68 | B、65 |
| C、-46 | D、-49 |
若定义在R上奇函数f(x)满足f(x)=f(x+5),且f(1)=1,f(2)=2,则f(3)-f(4)=( )
| A、-1 | B、1 | C、-2 | D、2 |
甲,乙,丙,丁四位同学各自对A,B两变量的线性相关试验,并用回归分析方法分别求得相关系数r如表:
则这四位同学的试验结果能体现出A,B两变量有更强的线性相关性的是( )
| 甲 | 乙 | 丙 | 丁 | |
| r | 0.82 | 0.78 | 0.69 | 0.85 |
| A、甲 | B、乙 | C、丙 | D、丁 |
复数(
+
i)2=( )
| ||
| 2 |
| ||
| 2 |
| A、-i | B、i | C、-1 | D、1 |