题目内容
已知样本数据{x1,x2,…,xn}的方差为a,则样本数据{2x1+1,2x2+1,…,2xn+1}的方差为 .
考点:极差、方差与标准差
专题:概率与统计
分析:首先设原数据的平均数为
,则新数据的平均数为2
+3,然后利用方差的公式计算得出答案.
. |
| x |
. |
| x |
解答:
解:设原数据的平均数为
,则新数据的平均数为2
+1,
则原数据的方差为
[(x1-
)2+(x2-
)2+…+(xn-
)2]=a,
∴新数据的方差为:
[(2x1+1-2
-1)2+(2x2+1-2
-1)2+…+(2xn+1-2
-1)2]
=4×
[(x1-
)2+(x2-
)2+…+(xn-
)2]=4a.
故新数据的方差为:4a
故答案为:4a
. |
| x |
. |
| x |
则原数据的方差为
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
∴新数据的方差为:
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=4×
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
故新数据的方差为:4a
故答案为:4a
点评:本题考查方差的定义,注意数据前后的变化是解决问题的关键,属基础题.

练习册系列答案
相关题目
复数z=i(1+i)的虚部是( )
| A、0 | B、1 | C、i | D、-1 |
变量y对x的回归方程的意义是( )
| A、表示y与x之间的函数关系 |
| B、表示y与x之间的线性关系 |
| C、反映y与x之间的真实关系 |
| D、反映y与x之间的真实关系达到最大限度的吻合 |
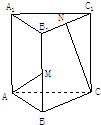 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|