题目内容
log
sin
π+log
cos
π的值是( )
| 2 |
| 5 |
| 12 |
| 2 |
| 5 |
| 12 |
| A、4 | B、1 | C、-4 | D、-1 |
考点:对数的运算性质,二倍角的正弦
专题:函数的性质及应用
分析:利用对数运算法则和二倍角的正弦公式求解.
解答:
解:log
sin
π+log
cos
π
=log
(sin
cos
)
=log
(
sin
)
=log
(
sin
)
=log
=-4.
故选:C.
| 2 |
| 5 |
| 12 |
| 2 |
| 5 |
| 12 |
=log
| 2 |
| 5π |
| 12 |
| 5π |
| 12 |
=log
| 2 |
| 1 |
| 2 |
| 5π |
| 6 |
=log
| 2 |
| 1 |
| 2 |
| π |
| 6 |
=log
| 2 |
| 1 |
| 4 |
=-4.
故选:C.
点评:本题考查对数的运算,是基础题,解题时要认真审题,注意正弦二倍角公式的合理运用.

练习册系列答案
相关题目
复数z=i(1+i)的虚部是( )
| A、0 | B、1 | C、i | D、-1 |
若复数2-bi(b∈R)的实部与虚部互为相反数,则b的值为( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
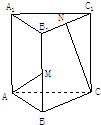 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等比数列{an}中,|a2|=2,a2014=-8a2011,a4<a1,则an=( )
| A、-(-2)n |
| B、-(-2)n-1 |
| C、(-2)n |
| D、(-2)n-1 |
等差数列8,5,2,…的第20项是( )
| A、68 | B、65 |
| C、-46 | D、-49 |
若定义在R上奇函数f(x)满足f(x)=f(x+5),且f(1)=1,f(2)=2,则f(3)-f(4)=( )
| A、-1 | B、1 | C、-2 | D、2 |
复数(
+
i)2=( )
| ||
| 2 |
| ||
| 2 |
| A、-i | B、i | C、-1 | D、1 |