题目内容
10.已知由不等式组$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤0}\\{x≥1}\end{array}\right.$所确定的平面区域为Ω,则能够覆盖区域Ω的最小圆的方程为(x-1)2+(y-2)2=1.分析 作出不等式组对应的平面区域,根据条件得到能够覆盖区域Ω的最小的圆是△ABC的外接圆,求出圆的方程即可.
解答 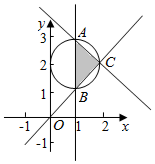 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
则△ABC为直角三角形,
则能够覆盖区域Ω的最小的圆是△ABC的外接圆,
由$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,即A(1,3),
由$\left\{\begin{array}{l}{x=1}\\{x-y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即B(1,1),
则AB的中点坐标为(1,2),半径R=1,
则对应圆的方程为(x-1)2+(y-2)2=1,
故答案为:(x-1)2+(y-2)2=1,
点评 本题主要考查线性规划的应用以及三角形外接圆的计算,作出不等式组对应的平面区域,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
15.点P到图形C上所有点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C的距离与到圆C外的定点A的距离相等的点的轨迹是( )
| A. | 射线 | B. | 椭圆 | C. | 双曲线的一支 | D. | 抛物线 |
2.离散型随机变量ξ的概率分布列如图,若Eξ=1,则Dξ的值为0.4.
| ξ | 0 | 1 | 2 |
| P | 0.2 | a | b |
19.函数$y=2sin({\frac{π}{2}x-\frac{π}{3}})({0≤x≤3})$的最大值与最小值之和为( )
| A. | $2-\sqrt{3}$ | B. | 0 | C. | -1 | D. | $-1-\sqrt{3}$ |
20.直角三角形ABC,三内角成等差数列,最短边的边长为m(m>0),P是△ABC内一点,并且∠APB=∠APC=∠BPC=120°,则PA+PB+PC=$\sqrt{21}$时,m的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |