题目内容
若集合A={x|x2-2x＜0}，B={x|x-1＞0}，则A∩B= ．
考点：交集及其运算
专题：集合
分析：求出A与B中不等式的解集确定出A与B，找出A与B的交集即可．
解答：
解：由A中不等式变形得：x（x-2）＜0，
解得：0＜x＜2，即A=（0，2），
由B中不等式解得：x＞1，即B=（1，+∞），
则A∩B=（1，2）．
故答案为：（1，2）
解得：0＜x＜2，即A=（0，2），
由B中不等式解得：x＞1，即B=（1，+∞），
则A∩B=（1，2）．
故答案为：（1，2）
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
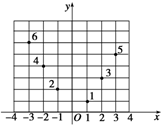如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{an}（n∈N*）的前12项，如下表所示．
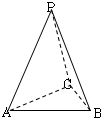在三棱锥P-ABC中，已知PA=PB=PC=2，∠BPA=∠BPC=∠CPA=30°，一绳子从A点绕三棱锥侧面一圈回到点A的距离中，绳子最短距离是将一个正四面体沿各棱的中点截去四个小三棱锥后得到一个新几何体，将此几何体的任意两个顶点连成一条线段，则其位于原四面体表面的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|