题目内容
已知P是
-
=1上的一点，F1、F2为双曲线的左右焦点，若P到F1的距离为14，则P到F2的距离为 ．
| x2 |
| 36 |
| y2 |
| 64 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义||PF1|-|PF2||=2a=12，已知|PF1|=14，进而可求|PF2|．
解答：
解：由题意，P在左支上，
利用双曲线的定义知||PF1|-|PF2||=2a=12，|PF1|=14，
故|PF2|=26或2．
∵P在左支上，
∴|PF2|=26．
故答案为：26．
利用双曲线的定义知||PF1|-|PF2||=2a=12，|PF1|=14，
故|PF2|=26或2．
∵P在左支上，
∴|PF2|=26．
故答案为：26．
点评：本题主要考查了双曲线的性质，运用双曲线的定义||PF1|-|PF2||=2a，是解题的关键，属基础题．
练习册系列答案
相关题目
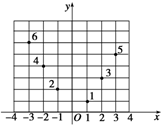如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{an}（n∈N*）的前12项，如下表所示．
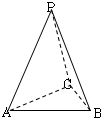在三棱锥P-ABC中，已知PA=PB=PC=2，∠BPA=∠BPC=∠CPA=30°，一绳子从A点绕三棱锥侧面一圈回到点A的距离中，绳子最短距离是