题目内容
7.已知双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为$\frac{2\sqrt{3}}{3}$.分析 利用已知条件,转化求解A到渐近线的距离,推出a,c的关系,然后求解双曲线的离心率即可.
解答 解:双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A(a,0),
以A为圆心,b为半径做圆A,圆A与双曲线C的一条渐近线交于M、N两点.
若∠MAN=60°,可得A到渐近线bx+ay=0的距离为:bcos30°=$\frac{\sqrt{3}}{2}b$,
可得:$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{3}}{2}b$,即$\frac{a}{c}=\frac{\sqrt{3}}{2}$,可得离心率为:e=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的简单性质的应用,点到直线的距离公式以及圆的方程的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
2.函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
| A. | [-2,2] | B. | [-1,1] | C. | [0,4] | D. | [1,3] |
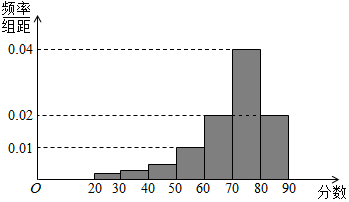
 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.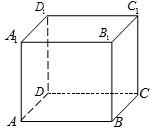 在正方体ABCD-A1B1C1D1中,给出下列结论:
在正方体ABCD-A1B1C1D1中,给出下列结论: