题目内容
16.已知数列{an}满足a1=$\frac{1}{5}$,且当n>1,n∈N*时,有an-1-an-4an-1•an=0.(1)求证:数列$\left\{{\frac{1}{a_n}}\right\}$为等差数列,并求出数列{an}的通项公式;
(2)令bn=an•an+1,设数列{bn}的前n项和为Sn,证明:${S_n}<\frac{1}{20}$.
分析 (1)通过将an-1-an=4an-1•an两边同时除以an-1•an、进而可知数列$\left\{{\frac{1}{a_n}}\right\}$是首项为5、公差为4的等差数列,利用等差数列的通项公式计算可得结论;
(2)通过(1)裂项可知bn=$\frac{1}{4}$($\frac{1}{4n+1}$-$\frac{1}{4n+5}$),进而并项相加放缩可得结论.
解答 证明:(1)因为an-1-an-4an-1•an=0,
所以an-1-an=4an-1•an,
两边同时除以an-1•an得:$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=4,
又因为$\frac{1}{{a}_{1}}$=5,
所以数列$\left\{{\frac{1}{a_n}}\right\}$是首项为5、公差为4的等差数列,
所以$\frac{1}{{a}_{n}}$=5+4(n-1)=4n+1,
所以an=$\frac{1}{4n+1}$;
(2)由(1)可知bn=an•an+1=$\frac{1}{4n+1}$•$\frac{1}{4n+5}$=$\frac{1}{4}$($\frac{1}{4n+1}$-$\frac{1}{4n+5}$),
所以Sn=$\frac{1}{4}$($\frac{1}{5}$-$\frac{1}{9}$+$\frac{1}{9}$-$\frac{1}{13}$+…+$\frac{1}{4n+1}$-$\frac{1}{4n+5}$)=$\frac{1}{4}$($\frac{1}{5}$-$\frac{1}{4n+5}$)<$\frac{1}{20}$,
即${S_n}<\frac{1}{20}$.
点评 本题是一道关于数列与不等式的综合题,考查数列的通项及前n项和,考查裂项相消法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案| A. | [-2,2] | B. | [-1,1] | C. | [0,4] | D. | [1,3] |
| A. | 1盏 | B. | 3盏 | C. | 5盏 | D. | 9盏 |
| A. | x=$\frac{2}{3}$π | B. | x=-$\frac{1}{12}$π | C. | x=$\frac{1}{3}$π | D. | x=$\frac{5}{12}$π |
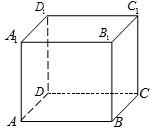 在正方体ABCD-A1B1C1D1中,给出下列结论:
在正方体ABCD-A1B1C1D1中,给出下列结论: