题目内容
8.椭圆$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,定点A($\frac{5}{3}$a,0),在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是[$\frac{1}{3}$,1).分析 由题意知|FP|=|FA|=$\frac{5}{3}$a-c,从而可得$\frac{5}{3}$a-c∈[a-c,a+c],从而解得.
解答 解:∵线段AP的垂直平分线过点F,
∴|FP|=|FA|=$\frac{5}{3}$a-c,
又∵|FP|∈[a-c,a+c],
∴$\frac{5}{3}$a-c∈[a-c,a+c],
∴a≤3c,
∴$\frac{1}{3}$≤e<1,
故答案为:[$\frac{1}{3}$,1).
点评 本题考查了圆锥曲线的定义的应用及椭圆的几何性质的应用,同时考查了转化的思想应用.

练习册系列答案
相关题目
3.已知正三棱锥的正视图和俯视如图所示,则其侧视图的面积为( )
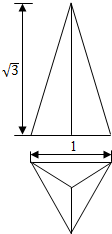

| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
13.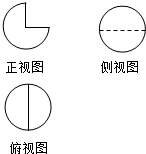 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )| A. | 14π | B. | 12π | C. | 10π | D. | 8π |
20.某几何体的三视图如图所示,在该几何体的各个面中,面积最小的面与底面的面积之比为( )
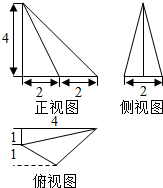

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
17.某几何体的三视图如图所示,则该几何体的体积是( )
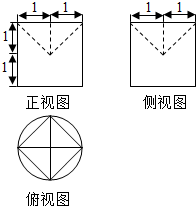

| A. | 2π-$\frac{2}{3}$ | B. | 2π-$\frac{4}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π-2 |
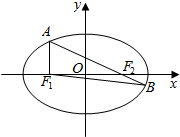 如图,点F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.
如图,点F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.