题目内容
(12分)已知数列 ,
, 满足
满足 ,
,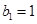 ,且
,且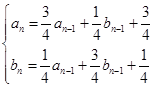 (
(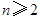 )
)
(Ⅰ)求数列 ,
, 的通项公式.
的通项公式.
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(Ⅰ)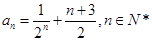 ,
,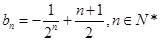 ;(Ⅱ)
;(Ⅱ)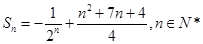 .
.
解析试题分析:(Ⅰ)本题的已知条件中, 、
、 在所满足的关系式中相互交叉表达,显然无法从现有已知条件中直接求出
在所满足的关系式中相互交叉表达,显然无法从现有已知条件中直接求出 、
、 的通项公式,所以必须通过构造新的数列来间接求解,再根据关系式中的系数特征可以看出,两个条件相加、减后得到的结果分别构成等差、等比数列,从而找到本题的突破口,接下来只需通过加、减消元即可得出所求;(Ⅱ)在(Ⅰ)中求得
的通项公式,所以必须通过构造新的数列来间接求解,再根据关系式中的系数特征可以看出,两个条件相加、减后得到的结果分别构成等差、等比数列,从而找到本题的突破口,接下来只需通过加、减消元即可得出所求;(Ⅱ)在(Ⅰ)中求得 的通项公式的基础上,只需借助相关前
的通项公式的基础上,只需借助相关前 项求和的恰当方法,不难得出所求.
项求和的恰当方法,不难得出所求.
试题解析:(Ⅰ)由题设得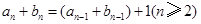 ,
,
可令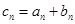 ,则
,则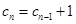 (
(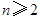 ),即
),即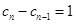 ,
,
所以 是首项为
是首项为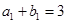 ,公差为1的等差数列,通项公式为
,公差为1的等差数列,通项公式为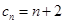 ,
,
由题设得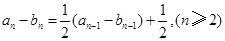 ,
,
可令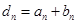 ,则
,则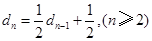 ,即
,即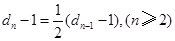 ,
,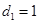 ,
,
所以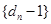 是首项为
是首项为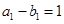 ,公比为
,公比为 的等比数列,通项公式为
的等比数列,通项公式为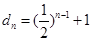 .
.
综上所述,可得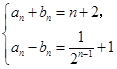 解之得:
解之得: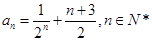 ;
;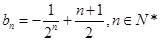 ;
;
(Ⅱ)由(Ⅰ)知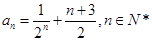 ,
,
显然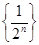 是首项为
是首项为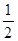 ,公比为
,公比为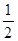 的等比数列,
的等比数列,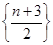 是首项为2,公差为
是首项为2,公差为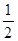 的等差数列,
的等差数列,
所以数列 的前
的前 和
和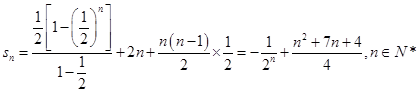 .
.
考点:数列的构造思想;等差、等比数列的定义、通项公式及前 项和;分组求和的方法;方程思想和发散思维.
项和;分组求和的方法;方程思想和发散思维.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 为虚数单位,且
为虚数单位,且 ,则
,则 的值为( )。
的值为( )。
| A.4 | B. | C. | D. |
直线 经过第一、第二和第四象限,则
经过第一、第二和第四象限,则 应满足( )
应满足( )
A. | B. | C. | D. |
若圆x2+y2=4上每个点的横坐标不变.纵坐标缩短为原来的 ,则所得曲线的方程是( )
,则所得曲线的方程是( )
A. | B. | C. | D. |
 .
. ,求bsinB+csinC的最小值.
,求bsinB+csinC的最小值. ,动点
,动点 与
与 分别在射线
分别在射线 上,且线段
上,且线段 的长为1,线段
的长为1,线段 分别是线段
分别是线段 的中点.
的中点.
 与
与 表示向量
表示向量 ;
; ,对于任意自然数
,对于任意自然数 都是递增数列,
都是递增数列, 的取值范围为 .
的取值范围为 .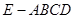 中,底面
中,底面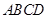 是正方形,
是正方形, 与
与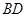 交于点
交于点 ,
,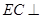 底面
底面 ,
, 为
为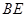 的中点.
的中点. 
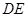 ∥平面
∥平面 ;
;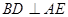 ;
; 在线段
在线段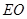 上是否存在点
上是否存在点 ,使
,使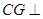 平面
平面 ?
?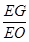 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. 的交点且平行于直线
的交点且平行于直线 的直线方程
的直线方程