题目内容
 如图,长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角,空间向量及应用
分析:建立空间直角坐标系,求向量
,
的坐标,根据向量夹角的余弦值的坐标公式,求这两向量夹角的余弦值,对所得余弦值加绝对值即得所求异面直线所成角的余弦值.
| AE |
| BC1 |
解答:
解:分别以边DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系,如下图,并能确定以下几点坐标:
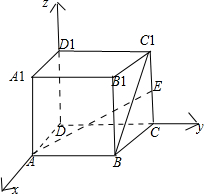 A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2);
A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2);
∴
=(-1,2,1),
=(-1,0,2);
∴设向量
与
夹角为θ,则:cosθ=
=
;
∴异面直线BC1与AE所成角的余弦值为:
.
故选D.
 A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2);
A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2);∴
| AE |
| BC1 |
∴设向量
| AE |
| BC1 |
| 1+2 | ||||
|
| ||
| 10 |
∴异面直线BC1与AE所成角的余弦值为:
| ||
| 10 |
故选D.
点评:本题考查建立空间直角坐标系,通过向量求异面直线所成角的余弦值的方法,两向量夹角的余弦公式.

练习册系列答案
相关题目
已知
=b+i(a,b∈R),其中i为虚数单位,则b-a=( )
| a+i |
| i |
| A、0 | B、1 | C、-2 | D、2 |
把复数z的共轭复数记作
,已知(1-2i)
=4-3i,则z=( )
. |
| z |
. |
| z |
| A、1-i | B、1+i |
| C、2-i | D、2+i |
曲线x2-y2=1经过伸缩变换T得到曲线
-
=1,那么直线x-2y+1=0经过伸缩变换T得到的直线方程为( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、2x-3y+6=0 |
| B、4x-6y+1=0 |
| C、3x-8y+12=0 |
| D、3x-8y+1=0 |
已知a=31.3,b=(
)-0.3,c=2log72,则a,b,c的大小关系为( )
| 1 |
| 3 |
| A、b<a<c |
| B、b<c<a |
| C、c<a<b |
| D、c<b<a |
已知直线l:y=k(x-2)(k>0)与抛物线C:y2=8x交于A,B两点,F为抛物线C的焦点,若|AF|=2|BF|,则k的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
若(1-2x)5展开式中的第2项小于第1项,且第2项不小于第3项,则实数x的取值范围是( )
A、x>-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PB中点,E为PC的中点,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PB中点,E为PC的中点,