题目内容
4.在一种称为“幸运35”的福利彩票中,规定从01,02,…,35这35个号码中任选7个不同号码组成一注.并通过摇奖机从这35个号码中摇出7个不同的号码作为特等奖,与特等奖号码仅6个相同的为一等奖,仅5个相同的为二等奖,仅4个相同的为三等奖,其他的情况不得奖,为了便于计算,假定每个投注号只有1次中奖钒机(只计奖金额最大的奖).该期的每组号码均有人买,且彩票无重复号码,若每注彩票为2元,特等奖奖金为100万元/注,一等奖奖金为1万元/注,二等奖奖金为100元/注,三等奖奖金为10元/注.试求;(1)奖金额X(元)的概率分布:;
(2)这一期彩票售完可以为福利事业筹集多少奖金?(不计发售彩票的费用).
分析 (1)由已知得X的可能取值为0,10,100,10000,1000000,分别求出相应的概率,由此能求出X的分布列.
(2)由已知利用组合数公式能求出这一期彩票售完可以为福利事业筹集奖金数.
解答 解:(1)由已知得X的可能取值为0,10,100,10000,1000000,
P(X=1000000)=$\frac{1}{{C}_{35}^{7}}$=$\frac{1}{6724520}$,P(X=10000)=$\frac{{C}_{7}^{6}}{{C}_{35}^{7}}$=$\frac{7}{6724520}$,
P(X=100)=$\frac{{C}_{7}^{5}}{{C}_{35}^{7}}$=$\frac{21}{6724520}$,P(X=10)=$\frac{{C}_{7}^{4}}{{C}_{35}^{7}}$=$\frac{35}{6724520}$,
P(X=0)=1-$\frac{1}{6724520}-\frac{7}{6724520}$-$\frac{21}{6724520}-\frac{35}{6724520}$=$\frac{6724456}{6724520}$,
∴X的分布列为:
| X | 0 | 10 | 100 | 10000 | 1000000 |
| P | $\frac{6724456}{6724520}$ | $\frac{35}{6724520}$ | $\frac{21}{6724520}$ | $\frac{7}{6724520}$ | $\frac{1}{6724520}$ |
${C}_{35}^{7}×2$=67783161600(元).
点评 本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
15.已知双曲线与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点重合,它们的离心率之和为$\frac{14}{5}$,则双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\frac{5}{3}x$ | C. | $y=±\frac{3}{5}x$ | D. | $y=±\sqrt{3}x$ |
16.设P={x|2x<16},Q={x|x2<4},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
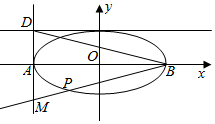 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.