题目内容
8.复数z=a3-2a+(m+a)i(a≥0,m∈R)的实部大于虚部,则m的取值范围为( )| A. | (-∞,-2) | B. | (-2,+∞) | C. | (-∞,0) | D. | (0,+∞) |
分析 由题意知a3-2a>m+a,a≥0,从而可得m<a3-3a在[0,+∞)上恒成立,令f(x)=x3-3x,求导判断函数的单调性并求最值即可.
解答 解:∵复数z=a3-2a+(m+a)i(a≥0,m∈R)的实部大于虚部,
∴a3-2a>m+a,a≥0,
即m<a3-3a在[0,+∞)上恒成立,
令f(x)=x3-3x,故f′(x)=3x2-3=3(x+1)(x-1),
故f(x)在[0,1)上是减函数,在[1,+∞)上是增函数,
故fmin(x)=f(1)=1-3=-2,
故m<-2,
故选:A.
点评 本题考查了导数的综合应用及复数的应用,同时考查了函数思想与转化思想的应用,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
19.已知c>0,设命题p:函数y=cx为减函数.命题q:当$x∈[{\frac{1}{2},2}]$时,函数f(x)=x+$\frac{1}{x}>\frac{1}{c}$恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围( )
| A. | $({0,\frac{1}{2}})$ | B. | $[{\frac{1}{2},1}]$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | (2,+∞) |
20.设a是实数,那么|a|<5成立的一个必要非充分条件是( )
| A. | a<5 | B. | |a|<4 | C. | a2<25 | D. | -5<a<5 |
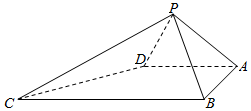 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.