题目内容
某四棱锥的三视图如图所示，则该四棱锥的体积是（ ）
| A、27 | ||
| B、9 | ||
C、3
| ||
| D、3 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何体是一个以俯视图为底面的四棱锥，分别计算棱锥的底面面积和高，代入可得几何体的体积．
解答：
解：由已知中的三视图可得，该几何体是一个以俯视图为底面的四棱锥，
棱锥的底面面积S=3×3=9，
棱锥的高h=1，
故棱锥的体积V=
Sh=3，
故选：D
棱锥的底面面积S=3×3=9，
棱锥的高h=1，
故棱锥的体积V=
| 1 |
| 3 |
故选：D
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．
练习册系列答案
口算能手系列答案
相关题目
已知f（x）=3x2+2x+1，若
f（x）dx=2f（a），那么a=（ ）
| ∫ | 1 -1 |
| A、-1 | ||
B、
| ||
C、-1或
| ||
| D、1 |
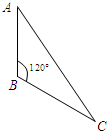在△ABC中，AB=3，BC=4，∠ABC=120°，若把△ABC绕直线AB旋转一周，则所形成的几何体的体积是（ ）| A、11π | B、12π |
| C、13π | D、14π |
现要制作一个圆锥形的漏斗，其母线长为l，要使其体积最大，高应为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
cos600°=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数y=ln（x+2）在点（-1，0）处的切线方程为（ ）
| A、x+y+1=0 |
| B、x-y+1=0 |
| C、x-2y+1=0 |
| D、x+2y+1=0 |