题目内容
15.某企业拟投入不超过450万元的资金购进一批总量不超过50台的生产设备,其中A设备每台售价13万元,可产生年利润4万元;B设备每台售价8万元,可产生年利润3万元,分别用x,y表示购进A设备和B设备的台数.(1)用x,y列出满足条件的数学关系式,并画出相应的平面区域;
(2)分别购进A设备和B设备多少台投入生产可获得最大年利润?最大年利润是多少万元?
分析 (1)设出变量,建立不等式关系,即可作出可行域.
(2)设出目标函数,利用平移直线法进行求解即可.
解答 解:(1)由已知x,y满足不等式$\left\{\begin{array}{l}{x+y≤50}\\{13x+8y≤450}\\{x≥0,y≥0}\\{x,y∈N}\end{array}\right.$,则不等式对应的平面区域为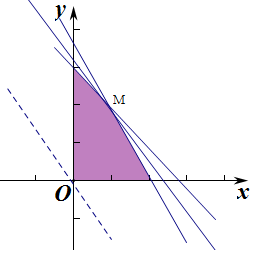
(2)设年利润为z万元,则目标函数为z=4x+3y,即y=-$\frac{4}{3}$x+$\frac{z}{3}$,
平移直线y=-$\frac{4}{3}$x+$\frac{z}{3}$,由图象得当直线经过点M时,直线的截距最大,此时z最大,
由$\left\{\begin{array}{l}{x+y=50}\\{13x+8y=450}\end{array}\right.$得$\left\{\begin{array}{l}{x=10}\\{y=40}\end{array}\right.$,即M(10,40),
此时z=4×10+3×40=160,
即分别购进A设备10台和B设备40台,投入生产可获得最大年利润,最大年利润是160万元.
点评 本题主要考查线性规划的应用,根据条件建立约束条件,作出可行域,利用平移法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.定义在实数域上的偶函数f(x)对于?x∈R,均满足条件f(x+2)=f(x)+f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)在(0,+∞)上恰有4个零点,则a的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
7.将函数y=cos(2x+$\frac{π}{6}$)图象上的点P($\frac{π}{4}$,t)向右平移m(m>0)个单位长度得到点P1,若P1位于函数y=cos2x的图象上,则( )
| A. | t=-$\frac{\sqrt{3}}{2}$,m的最小值为$\frac{π}{6}$ | B. | t=-$\frac{\sqrt{3}}{2}$,m的最小值为$\frac{π}{12}$ | ||
| C. | t=-$\frac{1}{2}$,m的最小值为$\frac{π}{12}$ | D. | t=-$\frac{1}{2}$,m的最小值为$\frac{π}{6}$ |
1.如果执行如图所示的程序框图,则输出的结果是( )


| A. | -4 | B. | -3 | C. | 2 | D. | 0 |
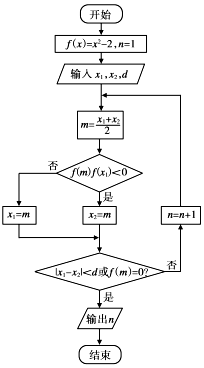 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )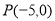 ,点
,点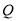 是圆
是圆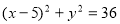 上的点,
上的点,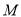 是线段
是线段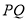 的中点.
的中点.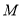 的轨迹
的轨迹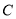 的方程;
的方程; 的直线
的直线 和轨迹
和轨迹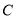 有两个交点
有两个交点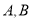 (
(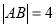 ,求直线
,求直线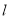 的方程.
的方程.