题目内容
17.函数y=$\sqrt{1-tan2x}$的定义域为($\frac{1}{2}$kπ-$\frac{π}{4}$,$\frac{1}{2}$kπ+$\frac{π}{8}$],k∈Z.分析 根据函数成立的条件建立不等式关系即可得到结论.
解答 解:要使函数有意义,则1-tan2x≥0,
即tan2x≤1,
即kπ-$\frac{π}{2}$<2x≤kπ+$\frac{π}{4}$,k∈Z,
即$\frac{1}{2}$kπ-$\frac{π}{4}$<x≤$\frac{1}{2}$kπ+$\frac{π}{8}$,
即函数的定义域为($\frac{1}{2}$kπ-$\frac{π}{4}$,$\frac{1}{2}$kπ+$\frac{π}{8}$],k∈Z,
故答案为:($\frac{1}{2}$kπ-$\frac{π}{4}$,$\frac{1}{2}$kπ+$\frac{π}{8}$],k∈Z.
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若直线l1:(a+1)x+a2y-3=0与直线l:2x+ay-2a-1=0平行,则a=( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 0或-1 |
12.在△ABC中,b2=ac,B=60°,则A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
2.已知正数x、y满足x+y=xy,则4x,y,$\frac{1}{x}$,$\frac{1}{y}$这4个数的平均数的( )
| A. | 最小值为2 | B. | 最小值为$\frac{5}{2}$ | C. | 最大值为2 | D. | 最大值为$\frac{5}{2}$ |
8.下列说法错误的是( )
| A. | 命题p:“?x0∈R,x02+x0+1<0”,则¬p:“?x∈R,x2+x+1≥0” | |
| B. | 命题“若x2-4x+3=0,则x=3”的逆否命题是假命题 | |
| C. | 命题“若m>0,则方程x2+x-m=0有实数根”的否定是“若m>0,则方程x2+x-m=0没有实数根” | |
| D. | 若p∧q为假命题,则p∨q为假命题 |
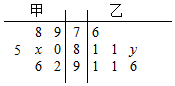 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.