Question

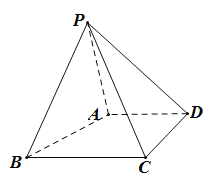
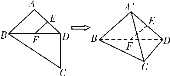
【题目】如图，平面四边形ABCD中，E、F是AD、BD中点，AB＝AD＝CD＝2， BD＝2 ，∠BDC＝90°，将△ABD沿对角线BD折起至△，使平面⊥平面BCD，则四面体中，下列结论不正确是 ( )

A. EF∥平面

B. 异面直线CD与所成的角为90°

C. 异面直线EF与所成的角为60°

D. 直线与平面BCD所成的角为30°

Answer 1

【答案】C

【解析】

根据线线平行判定定理、异面直线所成角、直线与平面所成角等知识对选项A、B、C、D进行逐一判断其正确与否.

解：选项A：因为E、F是AD、BD中点，

所以，

因为平面，

平面，

所以EF∥平面，

所以选项A正确；

选项B：因为平面⊥平面BCD，

平面平面BCD，

且∠BDC＝90°，即，

又因为平面BCD，

故平面，

故，

所以异面直线CD与所成的角为90°，

选项B正确；

选项C：由选项B可知平面，

所以，

因为AD＝CD＝2，

即＝CD＝2，

所以由勾股定理得，，

在中，

BC＝，

在中，

，

故，即，

因为，

所以，

故选项C错误；

选项D：连接

因为

所以

因为是中点，

所以，

因为平面⊥平面BCD，

平面平面BCD，

又因为平面，

故平面，

所以即为直线与平面BCD所成的角，

在中，，，

所以，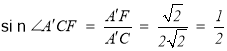

所以，

故直线与平面BCD所成的角为30°，

故选项D正确，

本题不正确的选项为C，故选C.