题目内容
【题目】在平面直角坐标系
内，动点
与两定点
， 
连线的斜率之积为
.
（1）求动点
的轨迹
的方程；
（2）设点
， 
是轨迹
上相异的两点.
（Ⅰ）过点
， 
分别作抛物线
的切线
， 
， 
与
两条切线相交于点
，证明： 
；
（Ⅱ）若直线
与直线
的斜率之积为
，证明： 
为定值，并求出这个定值.
【答案】（1）
（2）（Ⅰ）0（Ⅱ）1
【解析】试题分析：（1）直接有题意建立等式： 
得出轨迹方程（2）要证明
，则证明
即可，因为又是切线，所以根据
得到方程，从而得证（3）要求三角形面积是定值首先明确其表达式， 
，将其变量统一，最后化简得出定值
试题解析：
（1）依题意： 
（2）（Ⅰ）设直线
的斜率为
，设直线
的斜率为
，设切线为： 
，
， 
， 
.
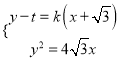
（Ⅱ）由条件得： 
， 
， 
.
.
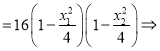
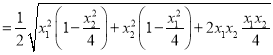
练习册系列答案
名校课堂系列答案
相关题目
