题目内容
【题目】下列判断正确的是（ ）
A.两圆锥曲线的离心率分别为
，则“
”是“两圆锥曲线均为椭圆”的充要条件.
B.已知
为圆
内异于圆心的一点，则直线
与该圆相交.
C.设
是实数，若方程
表示双曲线，则
.
D.命题
的否定是
.
【答案】D
【解析】
假设
,
,此时
,即可判断选项A；由点
与圆的位置关系可得
,再利用圆心到直线的距离与半径的关系的比较判断选项B；由双曲线的方程的判断选项C；由全称命题的否定的概念判断选项D.
对于选项A,若,,此时,但两圆锥曲线一个是椭圆,一个是双曲线,故A错误；
对于选项B,由
为圆
内异于圆心的一点可得,
又因为圆心到直线
的距离为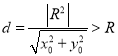
,所以圆与直线相离,故B错误；
对于选项C,若方程
表示双曲线,则
,则
或
,故C错误；
对于选项D,由全称命题的否定即可判断,故D正确；
故选:D
每课必练系列答案
【题目】某保险公司有一款保险产品的历史收益率（收益率
利润
保费收入）的频率分布直方图如图所示：
（1）试估计这款保险产品的收益率的平均值；
（2）设每份保单的保费在20元的基础上每增加
元，对应的销量为
（万份）．从历史销售记录中抽样得到如下5组
与
的对应数据：
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表，知
与
有较强的线性相关关系，且据此计算出的回归方程为
．
（ⅰ）求参数
的值；
（ⅱ）若把回归方程
当作
与
的线性关系，用（1）中求出的收益率的平均值作为此产品的收益率，试问每份保单的保费定为多少元时此产品可获得最大利润，并求出最大利润．注：保险产品的保费收入
每份保单的保费
销量．
【题目】司机在开机动车时使用手机是违法行为，会存在严重的安全隐患，危及自己和他人的生命. 为了研究司机开车时使用手机的情况，交警部门调查了
名机动车司机，得到以下统计：在
名男性司机中，开车时使用手机的有
人，开车时不使用手机的有
人；在
名女性司机中，开车时使用手机的有
人，开车时不使用手机的有
人．
（1）完成下面的
列联表，并判断是否有
的把握认为开车时使用手机与司机的性别有关；
开车时使用手机 | 开车时不使用手机 | 合计 | |
男性司机人数 | |||
女性司机人数 | |||
合计 |
（2）以上述的样本数据来估计总体，现交警部门从道路上行驶的大量机动车中随机抽检3辆，记这3辆车中司机为男性且开车时使用手机的车辆数为
，若每次抽检的结果都相互独立，求的分布列和数学期望
．
参考公式与数据：
参考数据：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式
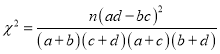span>，其中
.
