题目内容
11.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹马进行一场比赛,则田忌获胜的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 根据题意,设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,用列举法列举齐王与田忌赛马的情况,进而可得田忌胜出的情况数目,进而由等可能事件的概率计算可得答案
解答 解:设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,
从双方的马匹中随机选一匹进行一场比赛的所有的可能为Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc,
根据题设其中Ab,Ac,Bc是胜局共三种可能,
则田忌获胜的概率为$\frac{3}{9}$=$\frac{1}{3}$,
故选:A
点评 本题考查等可能事件的概率,涉及用列举法列举基本事件,注意按一定的顺序,做到不重不漏.

练习册系列答案
相关题目
1.设M为平面上以A(4,1),B(-1,-6),C(-3,2)三点为顶点的三角形区域(包括内部和边界),当点(x,y)在M上变化时,z=4x-3y的取值范围是( )
| A. | [-18,13] | B. | [0,14] | C. | [13,14] | D. | [-18,14] |
19.下列函数中在$(\frac{π}{4},\frac{3}{4}π)$上为减函数的是( )
| A. | y=2cos2x-1 | B. | y=-tanx | C. | $y=cos(2x-\frac{π}{2})$ | D. | y=sin2x+cos2x |
6.设$\overrightarrow{a}$,$\overrightarrow{b}$是两个非零向量,若命题p:$\overrightarrow{a}$•$\overrightarrow{b}$>0,命题q:$\overrightarrow{a}$,$\overrightarrow{b}$夹角是锐角,则命题p是命题q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16. 某商场在今年元宵节的促销活动中,对该天9时到14时的销售额进行统计,其频率分布直方图如图所示.已知9时到10时的销售额为5万元,则11时到13时的销售额为( )
某商场在今年元宵节的促销活动中,对该天9时到14时的销售额进行统计,其频率分布直方图如图所示.已知9时到10时的销售额为5万元,则11时到13时的销售额为( )
 某商场在今年元宵节的促销活动中,对该天9时到14时的销售额进行统计,其频率分布直方图如图所示.已知9时到10时的销售额为5万元,则11时到13时的销售额为( )
某商场在今年元宵节的促销活动中,对该天9时到14时的销售额进行统计,其频率分布直方图如图所示.已知9时到10时的销售额为5万元,则11时到13时的销售额为( )| A. | 20万元 | B. | 32.5万元 | C. | 35万元 | D. | 40万元 |
1.已知cos(α+$\frac{π}{2}$)=$\frac{3}{5}$,-$\frac{π}{2}$<α<$\frac{π}{2}$,则sin2α的值等于( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
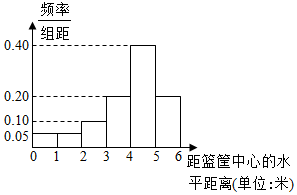 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图: