题目内容
9．若x，y满足约束条件$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{y≤2x+2}\end{array}}\right.$，则z=2x+y的最大值与最小值和等于（ ）| A． | -4 | B． | -2 | C． | 2 | D． | 6 |
分析 由约束条件作出可行域，数形结合得到最优解，把最优解的坐标分别代入目标函数求得最小值和最大值，则z=2x+y的最大值和最小值之和可求．
解答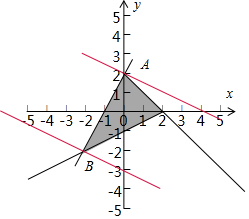 
解：由x，y满足约束条件$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{y≤2x+2}\end{array}}\right.$，作出可行域如图，
由图可知：A（0，2），由$\left\{\begin{array}{l}{x-2y-2=0}\\{y=2x+2}\end{array}\right.$解得B（-2，-2），
且A，B分别为目标函数z=2x+y取得最大值和最小值的最优解，
则zmin=-2×2-2=-6，zmax=2×0+2=2，
∴z=2x+y的最大值和最小值之和等于-4．
故选：A．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
相关题目
如图，四棱锥P-ABCD中，底面ABCD边长为4的正方形，PA=PD=2$\sqrt{2}$，平面PAD⊥平面ABCD．
14．设a=${∫}_{0}^{1}$xdx，b=1-${∫}_{0}^{1}$$\sqrt{x}$dx，c=${∫}_{0}^{1}$x3dx，则a，b，c的大小关系（ ）
| A． | b＞c＞a | B． | b＞a＞c | C． | a＞c＞b | D． | a＞b＞c |
1．复数${（{\frac{1}{2}+\frac{{\sqrt{3}}}{2}i}）^3}$的共轭复数是（ ）
| A． | -i | B． | i | C． | -1 | D． | 1 |
18．某中学调查了某班全部50名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
（I）从该班随机选1名同学，求该同学至少参加上述一个社团的概率；
（II）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1，A2，A3，A4，A5，3名女同学B1，B2，B3，现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率．
| 参加书法社团 | 未参加书法社团 | |
| 参加演讲社团 | 8 | 6 |
| 未参加演讲社团 | 6 | 30 |
（II）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1，A2，A3，A4，A5，3名女同学B1，B2，B3，现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率．