题目内容
设f(x)=3-|x-1|,则
f(x)dx= .
| ∫ | 2 -2 |
考点:定积分
专题:计算题,导数的综合应用
分析:把被积函数分段去掉绝对值,把要求的定积分转化为两个定积分的和,求出被积函数的原函数,分别代入积分上限和积分下限后作差得答案.
解答:
解:∵f(x)=3-|x-1|,
∴
f(x)dx=
(3-|x-1|)dx
=
(x+2)dx
(4-x)dx
=(
x2+2x)
+(4x-
x2)
=
+2-
×4+4+4×2-
×4-4+
=7.
故答案为:7.
∴
| ∫ | 2 -2 |
| ∫ | 2 -2 |
=
| ∫ | 1 -2 |
| +∫ | 2 1 |
=(
| 1 |
| 2 |
| | | 1 -2 |
| 1 |
| 2 |
| | | 2 1 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:7.
点评:本题考查了定积分的求法,当被积函数需要分段时,往往把要求的定积分转化为定积分的和,注意积分区间的改变,是基础题.

练习册系列答案
相关题目
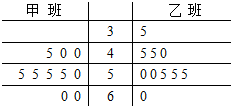 某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示: