题目内容
已知[x]表示不超过实数x的最大整数（x∈R），如：[-1.3]=-2，[0.8]=0，[3.4]=3．定义{x}=x-[x]，则：
（1）设函数f（x）=
，则函数y=f（x）-
x-
的不同零点有 个；
（2）{
}+{
}+{
}+…+{
}= ．
（1）设函数f（x）=
|
| 1 |
| 4 |
| 1 |
| 4 |
（2）{
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 20133 |
| 2014 |
| 20132014 |
| 2014 |
考点：分段函数的应用
专题：计算题,新定义,函数的性质及应用
分析：（1）画出函数f（x）的图象，画出直线y=
（x+1），通过图象观察即可判断函数零点的个数；
（2）通过二项式定理推得2013n=2014k+（-1）n，{
}=
（n为偶数）或
（n为奇数），即可得到答案．
| 1 |
| 4 |
（2）通过二项式定理推得2013n=2014k+（-1）n，{
| 2013n |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
解答：
解：（1）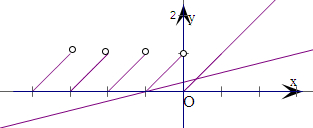
如图画出函数f（x）的图象，
画出直线y=
（x+1），通过图象观察，它们有两个交点，即函数y=f（x）-
x-
的不同零点有两个．
（2）2013n=（2014-1）n=2014n-C
2014n-1+
C
2014n-2+…+（-1）n=2014k+（-1）n，
∴
=k+
，{
}=
（n为偶数）或
（n为奇数）
∴{
}+{
}+{
}+…+{
}=（
+
）+（
+
）+…+（
+
）=1007．
故答案为：2，1007．
如图画出函数f（x）的图象，画出直线y=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
（2）2013n=（2014-1）n=2014n-C
1 n |
C
2 n |
∴
| 2013n |
| 2014 |
| (-1)n |
| 2014 |
| 2013n |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
∴{
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 20133 |
| 2014 |
| 20132014 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
故答案为：2，1007．
点评：本题考查分段函数的图象及应用，考查通过图象观察交点个数，判断函数零点个数，同时考查新定义的理解和运用，属于中档题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
