Question

8．已知圆C：（x-2）²+y²=4，点P在直线l：y=x+3上，若圆C上存在两点A、B使得$\overrightarrow{PA}$=3$\overrightarrow{PB}$，则点P的横坐标的取值范围是$[{\frac{{-1-\sqrt{7}}}{2}，\frac{{-1+\sqrt{7}}}{2}}]$．

Answer 1

分析 由题意可得圆心C（2，0），推导出点P到圆上的点的最小距离应小于或等于半径r=2．设点P的坐标为（m，m+3），则$\sqrt{（m-2）^{2}+（m+3{-0）}^{2}}$-2≤2，由此能求出点P的横坐标的取值范围．

解答 解：由题意可得圆心C（2，0），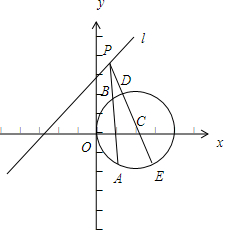
∵点P在直线l：y=x+3上，圆C上存在两点A、B使得$\overrightarrow{PA}$=3$\overrightarrow{PB}$，
如图，|AB|=2|PB|，|CD|=|CE|=r=2，
∴点P到圆上的点的最小距离|PD|应小于或等于半径r=2．
设点P的坐标为（m，m+3），
则$\sqrt{（m-2）^{2}+（m+3{-0）}^{2}}$-2≤2，
化简可得2m²+2m-3≤0，解得$\frac{-1-\sqrt{7}}{2}$≤m≤$\frac{-1+\sqrt{7}}{2}$，
∴点P的横坐标的取值范围是：$[{\frac{{-1-\sqrt{7}}}{2}，\frac{{-1+\sqrt{7}}}{2}}]$
故答案为：$[{\frac{{-1-\sqrt{7}}}{2}，\frac{{-1+\sqrt{7}}}{2}}]$．

点评 本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，判断点P到圆上的点的最小距离应小于或等于半径，是解题的关键，体现了转化的数学思想，属于中档题．